【Unity】【数学】視錐台（Frustum）について（第1回）

はじめに

こんばんは、代表の堂前です！

今回はUnityを利用した数学的な話をしようと思います。
取り上げる話題は「視錐台」（Frustum）についてです。

視錐台はカメラの見える範囲のことを指しますが、それを数学的に紐解いていきましょう。
（数回に分けて少しずつ進める予定です。）

※検証に利用したのはMacのUnity5.4.1f1になります。

---

視錐台とその構成

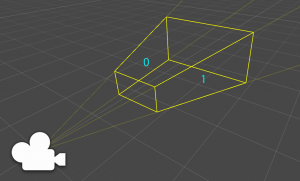
3Dの世界はカメラから覗いて映像を捉えるのですが、そこでいう視錐台は下図の濃い黄色の部分の様に一部だけ切り抜いた範囲の事を指します。

左下がカメラになっていて、そこから視界が広がるイメージです。
そして最終的には台形が立体になったもの（「四角錐台」と呼びます）の形になりますが、特徴的なのがカメラから見て手前と奥が切れているところです。
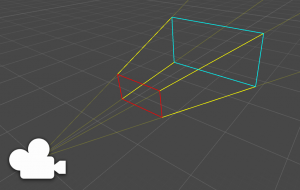
手前側が「Camera.nearClipPlane」になり、奥側が「Camera.farClipPlane」となります。

つまりnear面、far面となります。
下図ではそれぞれ赤い部分、水色の部分になります。

立体なのでそれぞれに「面」を持ちます。
パッと見で6つの面を持っているのがわかります。

左右	上下	前後

3Dでは視界関連で処理を考える際、視錐台を意識して行うものが幾つかあります。
例えば視錐台カリングなどがそうで、これは視錐台内に入っているかどうかを判定して処理を簡略化するものです。

その際にこの「面」の概念が必要になってきますが、Unityではそれを獲得する関数が存在します。
以下になります。

public static Plane[] GeometryUtility.CalculateFrustumPlanes(Camera camera);

この関数に「Camera」を渡すと、面に相当する「Plane」の配列が返ってきます。
6面あるので6要素の配列になり、それぞれが各面に対応しています。
対応は以下の通りです。（英語のドキュメントには載ってますね。）

要素	内容
0	左
1	右
2	下
3	上
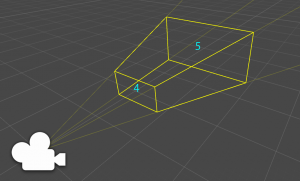
4	near面
5	far面

この「Plane」をどう使うかが重要になってきます。

---

Planeの構成

視錐台としてPlaneが6つ得られました。
このPlaneは数学的な「平面」の事を指します。

平面には「向き」があり、それを表すのに「法線」、つまり平面に垂直なベクトルの概念が必要になってきます。

（※Unityドキュメントより抜粋）

この視錐台の平面も例外ではありません。
それぞれに法線を持っていますが、どの様になっているかを見てみましょう。

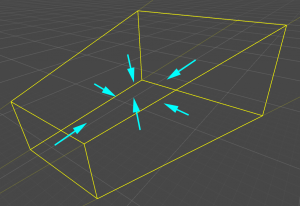
視錐台の平面の法線は（少なくともUnity上では）内向きになる様になっています。
これが視錐台での処理のキモになっていますが、次回に続きます。

---

 

 

【免責事項】
本サイトでの情報を利用することによる損害等に対し、株式会社ロジカルビートは一切の責任を負いません。