はじめに
こんばんは、代表の堂前です！
前回に引き続き、Unityを利用して「視錐台」（Frustum）の説明をしていきます。
今回は視錐台の内外判定が主な話題になります。
※検証に利用したのはMacのUnity5.4.1f1になります。
平面と距離
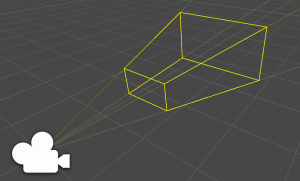
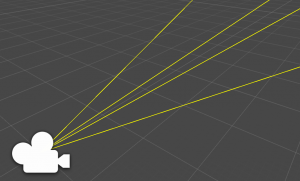
前回は視錐台が6つの平面（Plane）から構成されているという話をしました。
そしてその平面は、向きを表す法線を持っている事いうところまで説明しました。
今回はまず、平面自体に着目します。
平面関連の計算として、点と平面の距離を算出できます。
（UnityではPlane.GetDistanceToPoint()で獲得できます。）
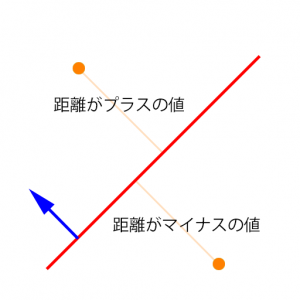
点から平面への最短距離（垂線）を測れますが、ここでポイントなのは、点が法線側がそうでないかで、得られる値もプラスもしくはマイナスが変わってきます。
基本的に法線側がプラス、そうでない方がマイナスで、Unityのは少なくともそうなっています。
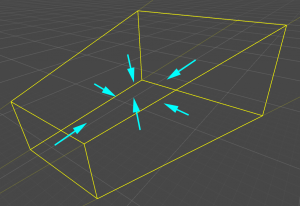
ここで視錐台に戻りますが、前回の最後で視錐台の平面は全て内向きになっていると説明しました。
ゲームではよく視界の中に物体等が入るかどうかという判定を行います。
これは「視錐台の中に入っているかどうか？」ということと合致します。
物体を崩して点と考えた際、とある点が視錐台の中に入るには、「全ての平面との距離がプラスの値になっている」必要があります。
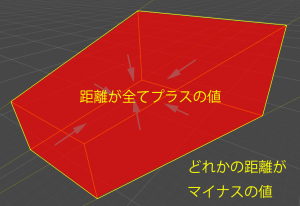
図形から見ると内外判定は非常に面倒そうに見えますが、その実は非常にシンプルな考えだと分かります。
Unityでの活用
視錐台の内外判定の原理が分かりましたが、Unityではそれを補助するための関数が用意されています。
以下になります。
public static bool GeometryUtility.TestPlanesAABB(Plane[] planes, Bounds bounds);
引数に平面（Plane）の配列と、バウンディングボックス（Bounds）を求められます。
点ではなく立体で判定する形式で、非常に便利です。
肝心のPlaneの配列ですが、GeometryUtility.CalculateFrustumPlanes()の結果をそのまま使うようなニュアンスが強いです。
しかし例えばゲーム的に「視界の中に入っているか？」という判定を行いたい時、near,far面は必ずしも必要とはいえず、むしろ取っ払ってしまった方が自然ですし、平面も4つで済むことが想像できます。
（測定はしていないですが、面が少ない方が処理速度も速いはずです。）
| near,farがあると6面必要 | near,farを取ると4面で済む |
 |  |
幸いnear,far面はPlaneの配列の最後の2つなので、下のようにリサイズして4つにすると良いでしょう。
// 視錐台平面を獲得
Plane[] planes = GeometryUtility.CalculateFrustumPlanes( camera );
System.Array.Resize( ref planes, 4 ); // near,far面を排除
// 内外判定
if ( GeometryUtility.TestPlanesAABB( planes, bounds ) ) {
// 入った！！
}これで内外判定が効率よく行えました。
次回も視錐台でネタが何かあれば・・・補足的に何か書きます。
【免責事項】
本サイトでの情報を利用することによる損害等に対し、株式会社ロジカルビートは一切の責任を負いません。
