はじめに
こんばんは、代表の堂前です!
前回は16ビットカラーの中身について取り上げました。
それについて挙動は説明したものの検証の部分などが抜けていたと感じましたので、今回は少し掘り下げて補足編としてお送りします。
(今回はUnityを使わず、数学的な内容寄りになっています。)
※今回は推測を多く含みますので、その点は念頭に置いて下さい。
動作保証
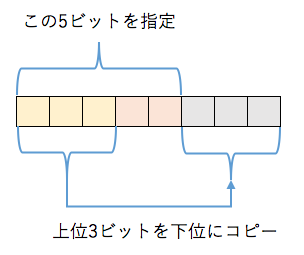
16ビットのカラー拡張について、動作原理は以下であると示しました。
ですが、必ずしもこうであるとは言い切れません!
というのも筆者の無駄に長い経験上、上記形式ではなく常に0を入れるタイプのハードウェアも触ったことがあります。
ですので推測ではありますが、どういう風に16ビットカラーが解釈されるかはGPUもしくはグラフィックスAPIによって変わるのではと思います。(この変換がどの部分で行われているかもよく分かっていません。)
しかしその一方で数値的な検証(次に記します)を行い、それを見てもこの形式がベストとも思えるので、これまた推測ではありますが、現在は大半がこの形式ではと思っています。
数値の確認
今回は5ビットのみで検証を行いますが、改めて上図の形式を数学的に考えます。
これをプログラムとして書くと以下のようになります。
C8 = (C5 << 3) | (C5 >> 2)
※C8・・・8ビットになった数値
C5・・・5ビットでの数値
ビットシフトと論理和(OR)を使って数値を算出しています。
C5は5ビットなので0〜31の値になり、これをC8として確認するにはプログラムを組んでもいいのですが、Excelでシミュレーションしてみます。
A列は5ビットの0〜31(すなわちC5)が、B列は8ビット後の数値(すなわちC8)が入っています。
そしてB列のExcelでの変換式は以下の通りになります。
(便宜上、引き続きC8とC5表記を利用しています。)
C8 = BITOR(BITLSHIFT(C5,3),BITRSHIFT(C5,2))
これでExcel上で確認出来るようになります。
結果を以下に改めて掲載します。
| 5ビットでの段階 (C5) |
8ビットでの変換 (C8) |
差分 |
| 0 | 0 | |
| 1 | 8 | 8 |
| 2 | 16 | 8 |
| 3 | 24 | 8 |
| 4 | 33 | 9 |
| 5 | 41 | 8 |
| 6 | 49 | 8 |
| 7 | 57 | 8 |
| 8 | 66 | 9 |
| 9 | 74 | 8 |
| 10 | 82 | 8 |
| 11 | 90 | 8 |
| 12 | 99 | 9 |
| 13 | 107 | 8 |
| 14 | 115 | 8 |
| 15 | 123 | 8 |
| 16 | 132 | 9 |
| 17 | 140 | 8 |
| 18 | 148 | 8 |
| 19 | 156 | 8 |
| 20 | 165 | 9 |
| 21 | 173 | 8 |
| 22 | 181 | 8 |
| 23 | 189 | 8 |
| 24 | 198 | 9 |
| 25 | 206 | 8 |
| 26 | 214 | 8 |
| 27 | 222 | 8 |
| 28 | 231 | 9 |
| 29 | 239 | 8 |
| 30 | 247 | 8 |
| 31 | 255 | 8 |
C5の0〜31に対しC8として0〜255が得られます。
これは前回の出力結果とも合致しています。
ここでずっと「差分」(C列)という項目が気になっているかと思います。
これはC5の現在の項目と前の項目で、C8の値がどれだけ増えたかの数値になります。
(例えばC5=3の場合、C8が16→24なので8となる。)
基本的にこの項目は8になりますが、時折9になっていて、それが定期的に来ているように見えます。
(8→8→8→9→8→8→8→9→8→8→8→9→・・・)
下位を常に0もしくは1にすると差分は必ず8になり、値の上の方もしくは下の方に隙間ができます。
イメージ的には差分にたまに9が来て、0〜255が表現できるようになっている、という感じでしょうか。
なぜこうなるかはよく理解できていない部分がありますが、規則正しく9が来ていることに、数学的な美しさと面白さを感じ取れます。
【免責事項】
本サイトでの情報を利用することによる損害等に対し、株式会社ロジカルビートは一切の責任を負いません。